Flow’s path to Permissionless Validators: Implementing Proof of Possession

Moving Towards Permissionless Participation: Flow’s Implementation of Proof of Possession

This article explains Flow’s recent implementation of Proof of Possession (PoP) for staking keys, a small but critical step in its decentralization roadmap [1]. The article covers why PoP is needed, what risks it prevents, and how it was implemented in Flow. Whether you’re a developer, validator, or simply curious about blockchain security, this post gives you a clear view of why PoP matters — with optional technical dives for those who want to explore the cryptography details.

1. The Vision and the Missing Guarantee

Flow is designed to become a permissionless network [1] where anyone can run a node and participate in consensus. That means validator registration needs to be simple, open, and secure, without requiring off-chain coordination or human oversight.

Until recently, the protocol allowed node operators to register a staking public key without proving they owned the corresponding private key. This works when registration is limited to trusted validators, but it left a gap: the system couldn’t cryptographically confirm that a node owns the staking private key and won’t threathen the protocol security.

While most validators honestly stake using keys they control, the protocol cannot rely on this assumption to prevent malicious behaviour. Private key ownership needs to be enforced and not just expected. The solution is to require a Proof of Possession (PoP): a cryptographic proof that ties each public key to a real private key before it becomes part of the network.

PoP aligns the staking mechanism with the protocol’s long-term goals [1]. It’s a small change to make validator participation truly permissionless and self-contained, without relying on trust.

2. Known Attack Vectors Without PoP

Flow relies on cryptographic pairing primitives in two areas: BLS multi-signature [2] for quorum certificates and block sealing, and SPoCK proofs for transaction verification and mitigating the Verifier’s dilemma [6]. Both currently rely on the assumption that each public key in the system was derived from a corresponding private key. Without a cryptographic proof of knowledge or possession, this assumption isn’t enforced.

Here is how the absence of a proof opens up technical vulnerabilities in each scenario:
‍

BLS Multi-Signature Forgery

Flow validators sign various messages using the BLS signature scheme, which can be aggregated into a single signature to reduce the signature size and signature verification time. This is particularly efficient when the signatures all use the same message.

If an attacker can register a specially crafted public key, they can exploit aggregation properties of BLS to create a valid aggregate signature over the same message, even if some participants didn’t sign it. This is a known vulnerability in BLS multi-signature schemes [2] and is referred to as a rogue key attack [3].

Let’s take a high-level look at how this attack works in general, without Flow-specific details:

Imagine honest Alice and malicious Oscar are part of a protocol that uses aggregated signatures. Oscar wants to convince everyone that both he and Alice signed a message M, even though Alice never did.

Here’s how he does it:

• Public keys are shared. Alice has already shared her public key pka.
• Oscar creates a special public key. He generates his own key pair (sko, pko) normally. Instead of pko , he shares pko - pka as his public key.

Think of public keys as numbers that can be added and subtracted. Here, Oscar subtracts Alice’s public key from his own.

• Oscar signs the message using his real private key sko , and shares this signature with the protocol, claiming it’s an aggregated signature from both him and Alice.
• Why verification succeeds? During verification, the protocol first aggregates the two public keys of the signers Oscar and Alice. Aggregating public keys means summing up the keys: (pko - pka) + pka . The result is just pko cancelling out the victim’s public key. In a second step, the signature is checked against the sum pko, which passes because Oscar genuinely signed with sko.

Oscar can use the same approach to make it look like himself, Alice and Bob (or a larger group) all signed M while in reality it was only him.

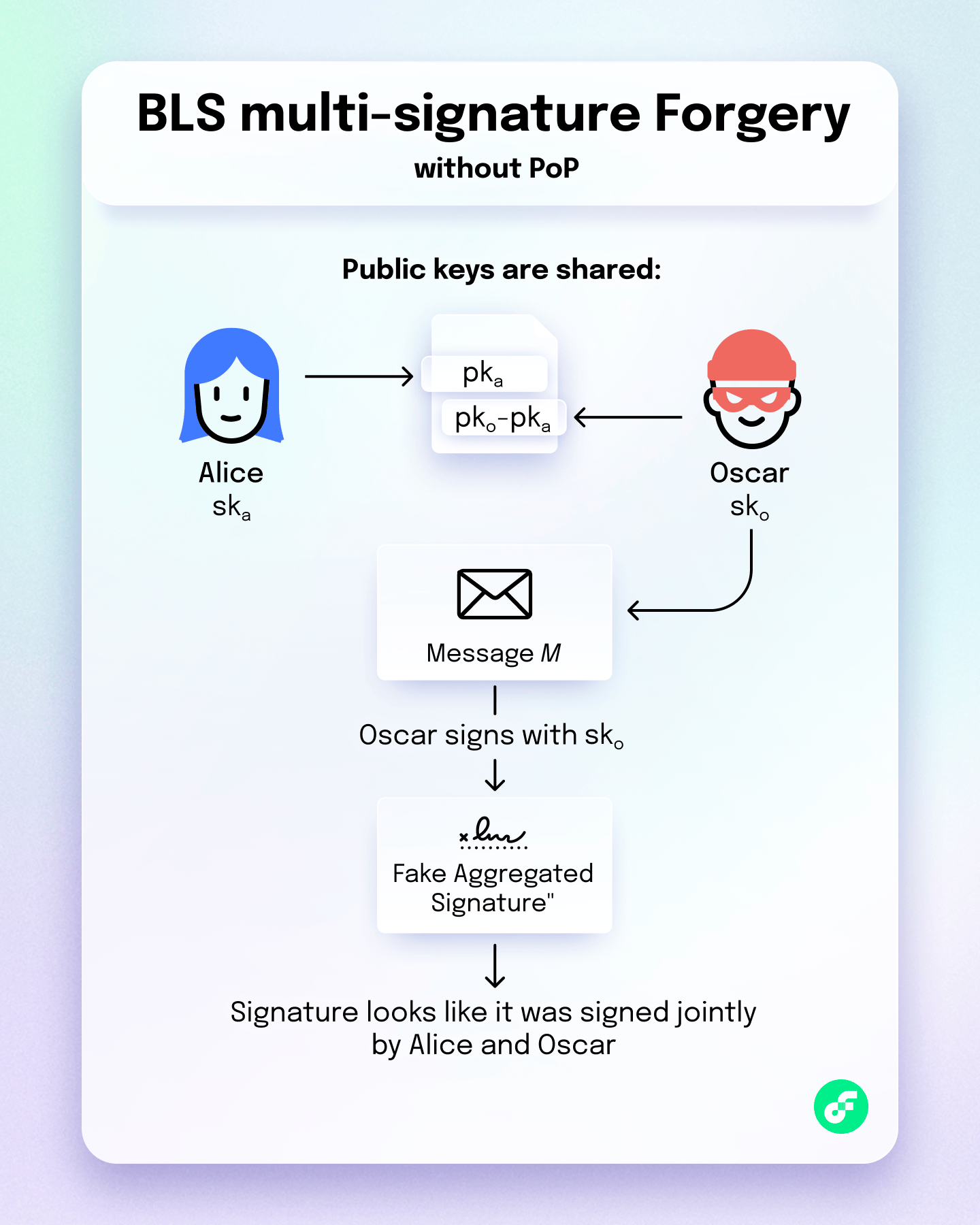
In Flow, a malicious collection node operator (playing Oscar’s role) can pretend that an entire collection cluster signed a certain collection. Similarly, a malicious consensus node can forge a fake block qurom certificate that looks like it was signed by a real quorum.

For both these attacks to succeed to fool other validators, the malicious node still has to bypass other protections in the Flow protocol, but the rogue public key vulnerability gives them a good start. The attack above wouldn’t work if Oscar is forced to show a proof that he knows the private key corresponding to his shared public key pko - pka , which he obviously doesn’t know and cannot compute.

BLS-SPoCK proof forgery

Flow uses a protocol based on BLS-SPoCK [6] to address the verifier’s dilemma, which describes the challenge of ensuring that validators check block results even though they are incentivized to skip resource-intensive work. To enforce these checks, each verifier must produce a personalized proof that they’ve executed the block themselves. Two SPoCK proofs are verifiable against each other using the two corresponding public keys, in order to convince a third party that the two provers computed the same execution trace from the block.

If the public keys used in this process do not correspond to actual private keys, the SPoCK proof guarantees do not hold. A verifier that crafts a rogue public key, can potentially bypass the transaction execution and submit a valid-looking proof without doing the work.This attack leverages the properties of pairings (the math used under the hood in the BLS-based SPoCK scheme) and undermines the core incentive in the protocol’s transaction verification.

To see an example of such an attack, we will need to remember how a SPoCK verification works in the first place. Warning: incoming math zone, If that’s not your thing today, go ahead and scroll past it. A SPoCK verification involves two public keys from Alice and Oscar,  pka and pko as well as two proofs proofa and proofo , and it checks the pairing equality e(proofa, pko) =?= e(proofo, pka) . If the equality holds, Alice and Oscar showed that they generated their proofs from the same secret M.

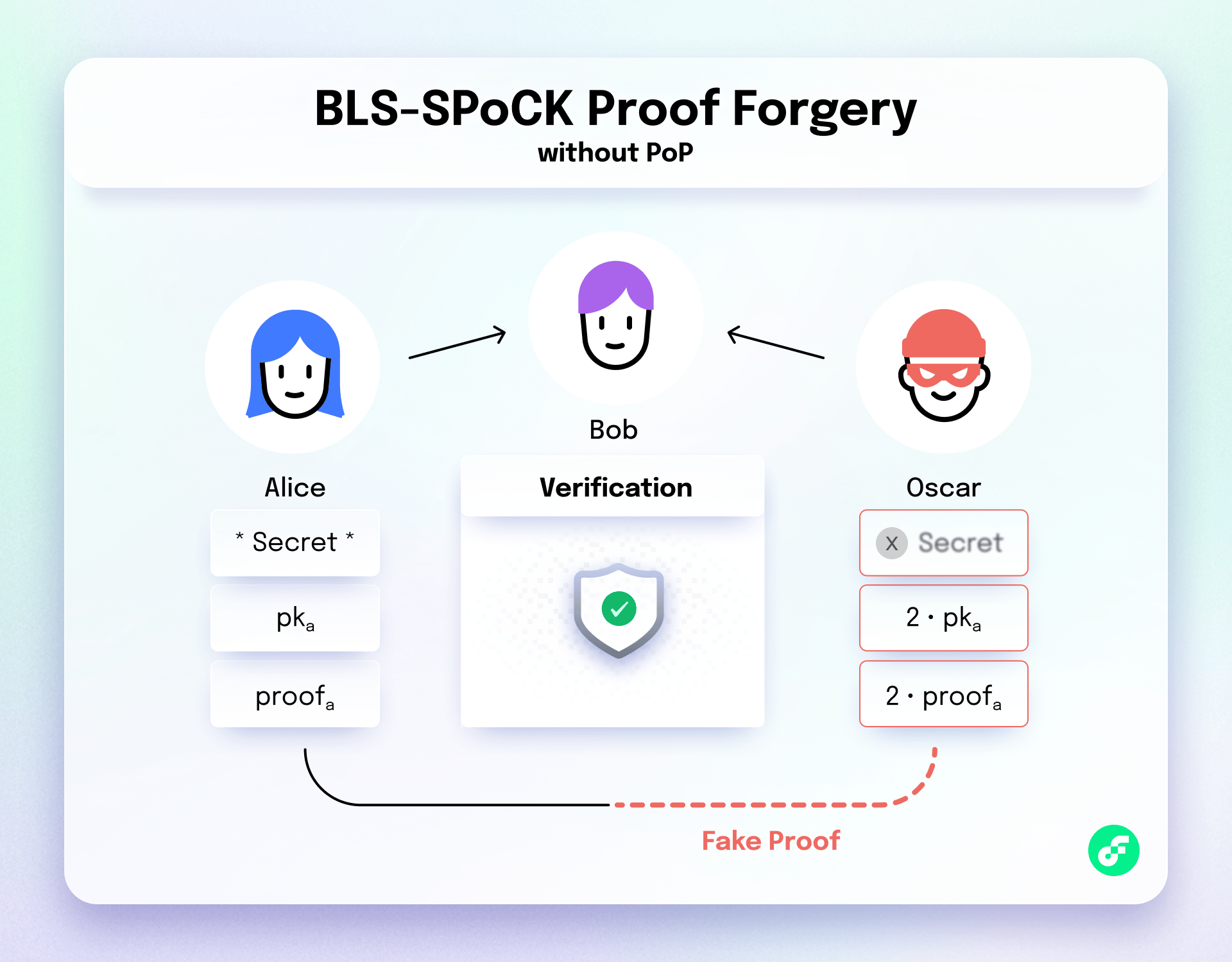
In the happy path where everyone is honest, pka and pko are respectively generated from private keys ska and sko , while proofa and proofo are the BLS signatures using respectively ska and sko of the secret execution trace M . The equality checks becomes e(ska . h(M), sko . g) =?= e(sko . h(M), ska . g) where g is the generator of the public keys subgroup, and h is the hash function used when signing. The pairing bilinearity e makes the equation hold, each side being equal to ska x sko . e(h(M),g).
If Oscar is malicious, and lazy to compute the trace M, he can craft a fake public key and then fake proof to pass the check above and convince the verifiers that he did the job. He can simply pick 2 . pka as his public key, and 2 . proofa as his proof.
The verifictaion check would be e(proofa, 2 . pka) =?= e(2 . proofa, pka) and both sides would be equal to 2. e(proofa, pka), again thanks to the pairing bilineraity.

Both of these examples rely on the same gap: accepting public keys without verifying that they were generated honestly from a private key. A rogue public key needs to be crafted using the other participants’ public keys. It’s not possible for the attacker to derive the private key from the crafted public key afterwards. The PoP computation is only possible using the private key, and that’s why PoP closes the gap with a simple, verifiable proof.

3. Proof of Possession: The Fix and the Guarantee

There are a few ways to mitigate the risks above:

• Prove knowledge of the secret key (KOSK) [2][3]: A protocol can require every user that registers a public key to prove they know the exact private key value, for instance by presenting its value to a trusted party. This assumption is obviously not feasible in practice because it exposes the private keys and relies on a central authority. A zero-knowledge flavour of KOSK is also possible but the assumption remains too strong while a simpler proof is preferred.
• In the case of BLS multi-signature, a possible mitigation is to use distinct messages for each signature [4], or use random exponents when aggregating signatures and public keys [5]. We won’t cover the technical details of these mitigations in this post and refer curious readers to check [5] for a deeper dive. Both mitigations are costly and undermine the optimization benefits that BLS is meant to provide in the first place. Moreover, neither works to secure SPoCK.
• Prove possession of the secret key (PoP) [3]: A simpler solution that preserves the other advantages of pairing-based cryptography is to enforce users at the point of key registration to present a proof of possessing the secret key. This is a different type of proof than KOSK, where “possession” implies a slightly weaker but more flexible meaning than “knowledge”. A proof is a simple signature over the registered public key. Presenting a PoP is the realistic assumption and suitable to implement in protocols where public keys are registered once per user and have a relatively long lifetime like in proof of stake protocols.

4. How It Is Implemented Under the Hood

Flow’s implementation of Proof of Possession is simple, efficient, and integrated directly into the staking transaction process.

Signing the public key

When a node operator registers a staking public key, they must now include a signature over that public key using their corresponding private key. A specific domain separation tag for PoPs is used to create hash algorithms that are orthogonal to the ones used within the protocol (this is recommended in the BLS IRTF specifications [7] and a deeper dive can be found in [3]).

On-Chain Verification

The PoP is provided as part of the staking transaction along with the rest of public staking info. All this data is submitted by the node validator attempting to register to the network. The staking contract performs the verification directly on-chain, and checks that the PoP indeed matches the presented public key. The Cadence programming language has a built-in BLS verification function and has access to the specific PoP orthogonal hasher.

If this check fails, the staking request is rejected. If it passes, the validator is accepted into the staking pool. No off-chain logic or external coordination is required.

To support this, the staking transaction now requires a new argument which is the PoP value. This is the only visible change for node operators. The rest of the staking logic remains unchanged.

PoPs Are Not Stored On-Chain

Proofs of Possession are validated during staking registration, are not stored in the protocol state. Once a PoP has been verified and the staking request is accepted, the protocol  guarantees that the registered public key is valid, for as long as the node remains staked.

This design choice keeps the protocol state minimal and efficient. External clients do not need to query and re-verify PoPs themselves. By using certified and verified protocol states, which include the staking public keys, clients can be confident that all registered keys were backed by valid PoP proofs, without requiring persistent on-chain storage of the proofs.

For existing nodes admitted under the earlier trusted setup, social vetting by the governance committee provides equivalent assurance on the registered public key.

As a result, PoP validation is enforced only for new staking registrations. This approach maintains compatibility with the current validator set while moving the protocol toward stricter guarantees for future permissionless participation.

References

• [1] Flow protocol autonomy roadmap
• [2] Alexandra Boldyreva. Threshold signatures, multisignatures and blind signatures based on the gapdiffie-hellman-group signature scheme (PKC 2003)
• [3] Thomas Ristenpart, Scott Yilek. The Power of Proofs-of-Possession:Securing Multiparty Signatures against Rogue-Key Attacks (Eurocrypt 2007)
• [4] Dan Boneh, Craig Gentry, Ben Lynn, and Hovav Shacham. Aggregate and Verifiably Encrypted Signatures from Bilinear Maps (Eurocrypt 2003)
• [5] Dan Boneh, Manu Drijvers, and Gregory Neven. Compact Multi-Signatures for Smaller Blockchains (2018)
• [6] Tarak Ben Youssef, Riad S. Wahby. Specialized Proof of Confidential Knowledge (SPoCK) (2020)
• [7] CFRG - IRTF draft.  BLS Signatures

‍