Ethereum Merkle Patricia Trie Explained
Introduction
Merkle Patricia Trie is one of the key data structures for the Ethereum’s storage layer. I wanted to understand how exactly it works. So I did a deep research on all the materials I could find and implemented the algorithm myself.
In this block post, I’ll share what I have learned. Explain how exactly Merkle Patricia Trie works, and show you a demo of how a merkle proof is generated and verified.
The source code of the algorithm and the examples used in this blog post are all open sourced.
zhangchiqing/merkle-patricia-trie
This is a simplified implementation of Ethereum's modified Merkle Patricia Trie based on the Ethereum's yellow paper…
github.com
OK, let’s get started.
A basic key-value mapping
Ethereum’s Merkle Patricia Trie is essentially a key-value mapping that provides the following standard methods:
An implementation of the above Trie interface should pass the following test cases:
(Test cases in this tutorial are included in the repo and passed.)
Verify Data Integrity
What is merkle patricia trie different from a standard mapping?
Well, merkle patricia trie allows us to verify data integrity. (For the rest of this tutorial, we will call it trie for simplicity)
One can compute the Merkle Root Hash of the trie with the Hash function, such that if any key-value pair was updated, the merkle root hash of the trie would be different; if two Tries have the identical key-value pairs, they should have the same merkle root hash.
Let’s explain this behavior with some test cases:
Verify the inclusion of a key-value pair
Yes, the trie can verify data integrity, but why not simply comparing the hash by hashing the entire list of key-value pairs, why bother creating a trie data structure?
That’s because trie also allows us to verify the inclusion of a key-value pair without the access to the entire key-value pairs.
That means trie can provide a proof to prove that a certain key-value pair is included in a key-value mapping that produces a certain merkle root hash.
This is useful in Ethereum. For instance, imagine the Ethereum world state is a key-value mapping, and the keys are each account address, and the values are the balances for each account.
As a light client, which don’t have the access to the full blockchain state like full nodes do, but only the merkle root hash for certain block, how can it trust the result of its account balance returned from a full node?
The answer is, a full node can provide a merkle proof which contains the merkle root hash, the account key and its balance value, as well as other data. This merkle proof allows a light client to verify the correctness by its own without having access to the full blockchain state.
Let’s explain this behavior with test cases:
A light client can ask for a merkle root hash of the trie state, and use it to verify the balance of its account. If the trie was updated, even if the updates was to other keys, then the verification would fail.
And now, the light client only needs to trust the merkle root hash, which is a small piece of data, to convince themselves whether the full node returned the correct balance for its account.
OK, but why should the light client trust the merkle root hash?
Since Ethereum’s consensus mechanism is Proof of Work, and the merkle root hash for the world state is included in each block head, the computation work is the proof for verifying/trusting the merkle root hash.
It’s pretty cool that small as the merkle root hash can be used to verify the state of a giant key-value mapping.
Verify the implementation
I’ve explained how merkle patricia trie works. This repo provides a simple implementation. But, how can we verify our implementation?
An easy way is to verify with the Ethereum mainnet data and the official Trie golang implementation.
Ethereum has 3 Merkle Patricia Tries: Transaction Trie, Receipt Trie and State Trie. In each block header, it includes the 3 merkle root hashes: transactionRoot, receiptRoot and the stateRoot.
Since the transactionRoot is the merkle root hash of all the transactions included in the block, we could verify our implementation by taking all the transactions, then store them in our trie, compute its merkle root hash, and in the end compare it with the transactionRoot in the block header.
For instance, I picked the block 10467135 on mainnet, and saved all the 193 transactions into a transactions.json file.
Since the transaction root for block 10467135 is 0xbb345e208bda953c908027a45aa443d6cab6b8d2fd64e83ec52f1008ddeafa58. I can create a test case that adds the 193 transactions of block 10467135 to our Trie and check:
- Whether the merkle root hash is bb345e208bda953c908027a45aa443d6cab6b8d2fd64e83ec52f1008ddeafa58.
- Whether a merkle proof for a certain transaction generated from our trie implementation could be verified by the official implementation.
But what would be the keys and values for the list of transactions? The keys are the RLP encoding of a unsigned integer starting from index 0; the values are the RLP encoding of the corresponding transactions.
OK, let’s see the test cases:
The above test cases passed, and showed if we add all the 193 transactions of block 10467135 to our trie, then the trie hash is the same as the transactionRoot published in that block. And the merkle proof for the transaction with index 30, generated by our trie, is considered valid by official golang trie implementation.
Merkle Patricia Trie Internal — Trie Nodes
Now, let’s take a look at the internal of the trie.
Internally, the trie has 4 types of nodes: EmptyNode, LeafNode, BranchNode and ExtensionNode. Each node will be encoded and stored as key-value pairs in the a key-value store.
As an example, let’s take a look at Block 10593417 on mainnet to show how a transaction trie was built and how is it stored.
Block 10593417 only has 4 transactions with the transactionRoot hash: 0xab41f886be23cd786d8a69a72b0f988ea72e0b2e03970d0798f5e03763a442cc. So to store the 4 transactions to a trie, we are actually storing the following key-value pairs in hex-string form:
80 is the hex form of the bytes from the result of RLP encoding of unsigned integer 0: RLP(uint(0)). 01 is the result of RLP(uint(1)), and so on.
The value for key 80 is the result of RLP encoding of the first transaction. The value for key 01 is for the second transaction, and so on.
So we will add the above 4 key-value pairs to the trie, and let’s see how the internal structure of the trie changes when adding each of them.
To be more intuitive, I will use some diagrams to explain how it works. You could also inspect the state of each step by adding logs to the test cases.
Empty Trie
The trie structure contains only a root field pointing to a root node. And the Node type is an interface, which could be one of the 4 types of nodes.
When a trie is created, the root node points to an EmptyNode.
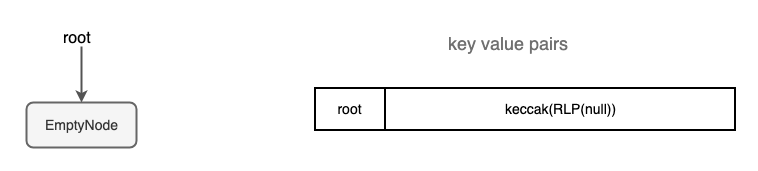
Adding the 1st transaction
When adding the key-value pair of the 1st transaction, a LeafNode is created with the transaction data stored in it. And the root node is updated to point to that LeafNode.
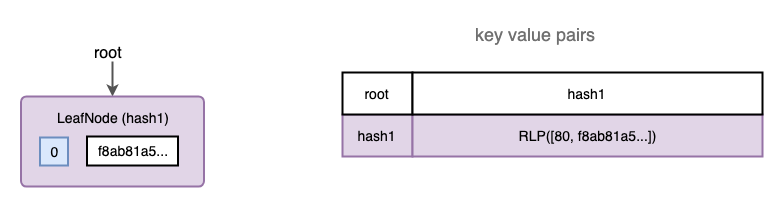
Adding the 2nd transaction
When adding the 2nd transaction, the LeafNode at the root will be turned into a BranchNode with two branches pointing to the 2 LeafNodes. The LeafNode on the right side holds the remaining nibbles (nibbles are a single hex character) — 1, and the value for the 2nd transaction.
And now the root node is pointing to the new BranchNode.
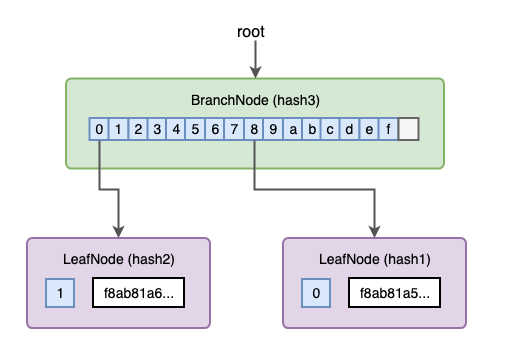
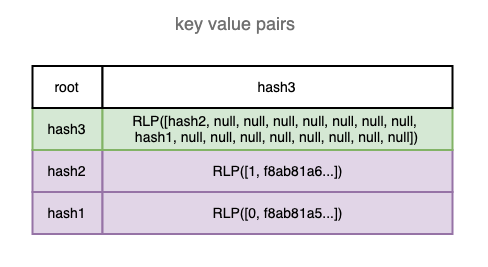
Adding the 3rd transaction
Adding the 3rd transaction will turn the LeafNode on the left side to be a BranchNode, similar to the process of adding the 2nd transaction. Although the root node didn’t change, its root hash has been changed, because it’s 0 branch is pointing to a different node with different hashes.
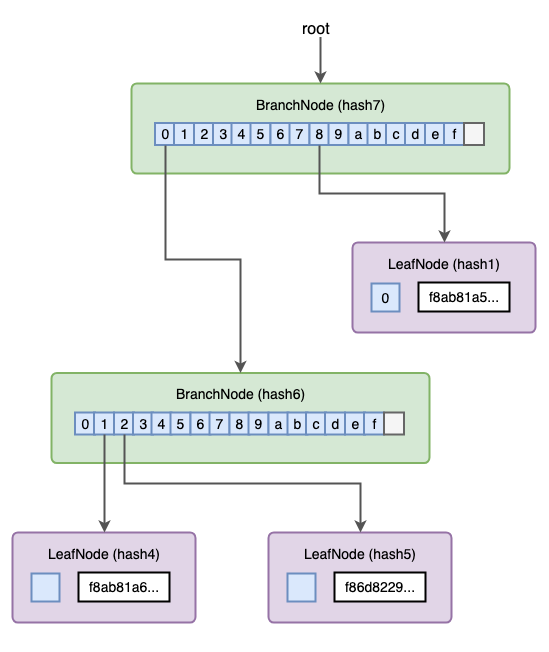
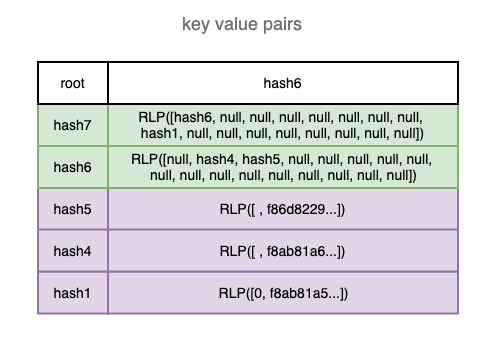
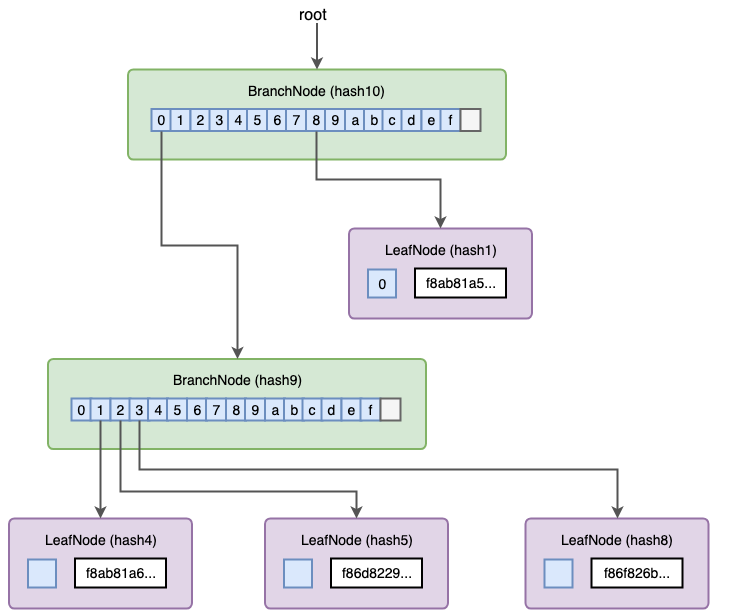
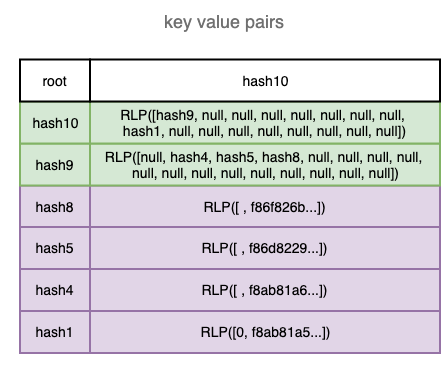
Adding the 4th transaction
Adding the last transaction is similar to adding the 3rd transaction. Now we can verify the root hash is identical to the transactionRoot included in the block.
Getting Merkle Proof for the 3rd transaction
The Merkle Proof for the 3rd transaction is simply the path to the LeafNode that stores the value of the 3rd transaction. When verifying the proof, one can start from the root hash, decode the Node, match the nibbles, and repeat until find the Node that matches all the remaining nibbles. If found, then the value is the one paired with the key; if not found, then the merkle proof is invalid.
The rule of updating the trie
In the above example, we’ve built a trie with 3 types of Nodes: EmptyNode, LeafNode and BranchNode. However, we didn’t have the chance to use ExtensionNode. Please find other test cases that use the ExtensionNode.
In general, the rule is:
- When stopped at an EmptyNode, replace it with a new LeafNode with the remaining path.
- When stopped at a LeafNode, convert it to an ExtensionNode and add a new branch and a new LeafNode.
- When stopped at an ExtensionNode, convert it to another ExtensionNode with shorter path and create a new BranchNode points to the ExtensionNode.
There are quite some details, if you are interested, you can read the source code.
Summary
Merkle Patricia Trie is a data structure that stores key-value pairs, just like a map. In additional to that, it also allows us to verify data integrity and the inclusion of a key-value pair.
More
Merkle Trie is heavily used in Ethereum storage, if you are interested in learning more, check out my blog post series:


