Uniswap V2 Explained (Beginner Friendly)
Among those keywords about the core tech and mechanisms in crypto mentioned by Vitalik, what is x*y=k? It looks quite simple. Isn’t it?
Yes it is. In fact, it’s the formula that drives decentralized exchanges. For instance, It is being used by Uniswap, an active decentralized cryptocurrency exchange on Ethereum.
Uniswap
Uniswap allows anyone to make market and swap tokens. The first version — Uniswap V1, was released in 2018 as a proof of concept. Version 2 was a production version released in 2020. And Version 3, which is currenty the latest version, was launched in 2021.
In this blog post, I will explain how Uniswap V2 works with examples that walk through basic scenarios, and how the simple but powerful formula works.
I believe having a good understanding of Uniswap V2 and its core idea makes it much easier to understand the latest version V3 and the mechanism of other decentralized exchanges.
Let’s get started.
Liquidity Pool
Uniswap V2 allows traders to directly swap from one ERC-20 token to another ERC-20 token. Traders don’t trade directly with each other. Instead, they trade with a token pool that has both tokens reserved. This token pool is called “Liquidity Pool”. But the question is where are the tokens reserved in the pool originally from?
The tokens in the liquidity pool are added by users, called “Liquidity Providers”.
Why do “Liquidity Provider” add their tokens to Liquidity Pool? Because they can earn fees when traders swap their tokens with the Liquidity Pool. We will see later.
Each Uniswap liquidity pool is a trading venue for a pair of ERC-20 tokens. Since there are lots of pairs, Uniswap will route the traders and liquidity providers to the corresponding liquidity pool for their transactions.
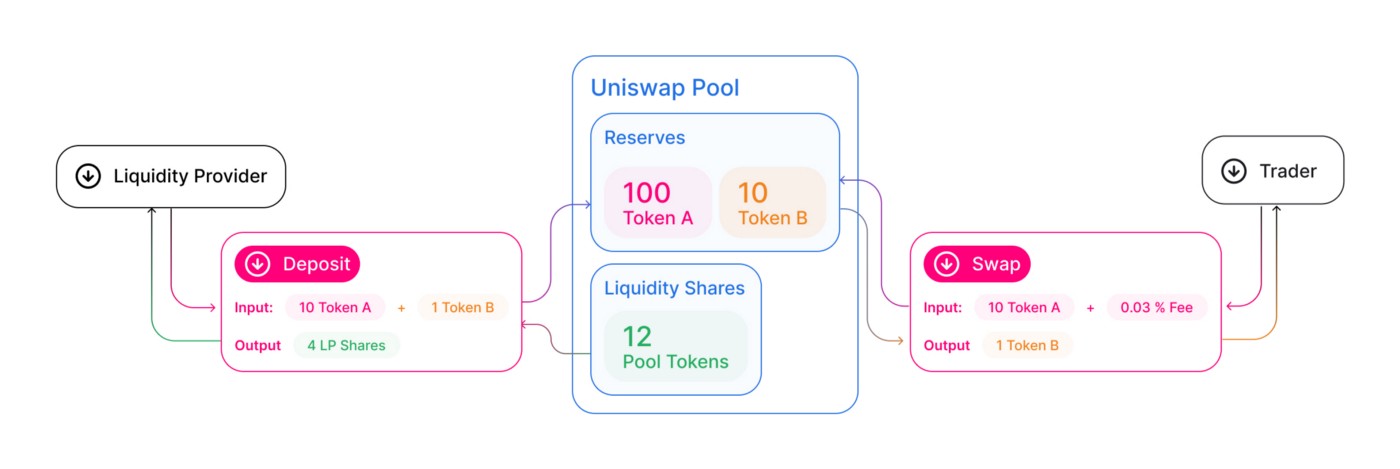
(source: https://docs.uniswap.org/protocol/V2/concepts/protocol-overview/how-uniswap-works)
OK, enough theories. Let’s go through an example as a trader, and see how they swap tokens with Uniswap.
Example — Trader Swap Tokens
Assume there are two types of ERC-20 tokens: tokenA and tokenB, and there is a Uniswap liquidity pool which has been created for swapping between tokenA and tokenB. We will explain how it is created later. For now, let’s say this tokenA-tokenB liquidity pool currently has 5 tokenA and 20 tokenB in it, so the ratio is 1 tokenA : 4 tokenB. And we assume that’s the current market ratio, meaning 1 tokenA is now worth 4 tokenB.
OK, now if trader Tim swaps his 1 tokenA for tokenB, the pool will take his 1 tokenA, transfer a certain amount of tokenB from the pool to Tim.
But how many tokenB will Tim receive after the swap? 4 tokenB? No, he will actually receive a bit less: 3.324996 tokenB instead. Uniswap determines the output token amount by using a constant product formula:
The constant product formula requires the trades should not change the product (K) of a pair’s reserved balances (X and Y). Let’s walk through the calculation step by step.
Originally, the liquidity pool has 5 tokenA and 20 tokenB, so X = 5 and Y = 20. when Tim swaps 1 tokenA, he will pay a 0.3% fee first, which is 0.003 tokenA (0.3% * 1). After the fee is paid, the remaining tokenA, which is 0.997 tokenA, will be swapped for tokenB, so the new X becomes 5.997 tokenA. Since K must remain unchanged, the new Y can be calculated from the formula X * Y = newX * newY. So newY is 16.675004 (X * Y / newX = 5 * 20 / 5.997 = 16.675004). This means the pool will hold 16.675004 tokenB, the remaining tokenB will be sent to Tim, which means Tim will receive 3.324996 tokenB (Y — newY = 20 – 16.675004 = 3.324996). After the swap, the pool has 6 tokenA and 16.675004 tokenB.
There are two things worth to mention in the above example:
Fixed rate
The fee is a fixed rate for each swap transaction, and is the same for any token pair swapping. As of right now, the rate is fixed as 0.3%. There is also a protocol fee, but it’s set as 0 currently, so I simply ignored it here.
V1 formula
For simplicity, the calculation steps I’m using here is actually from Uniswap V1, where the trading fee is applied by reducing the amount paid into the contract by 0.3% before enforcing the constant-product invariant:
Uniswap V2 formula is slightly different from V1 because it supports Flash Swap, which allows more advanced use cases, like borrowing the tokens from the pool first then returning them back within the same transaction. This introduces the possibility that swapping tokenA for tokenB might end up receiving some additional tokenA, in which case fee should also be charged.
However, our example is a typical use case for traders to swap one token for another, since the end result is the same as using V1’s formula, I decided to explain the calculation with V1’s formula for simplicity.
If you are interested in the details of V2 formula, you can read its whitepaper and source code linked at the end of this post.
The Economic model behind the formula
In summary, Tim swapped 1 tokenA for 3.324996 tokenB, and paid 0.003 tokenA as the fee. The swap caused tokenA’s price to drop from 4 tokenB to 3.324996 tokenB. In fact, if Tim continues to swap tokenA for tokenB, tokenA’s price will keep dropping. See the following table for the price change if Tim made 5 transactions to swap 1 tokenA for tokenB each time:
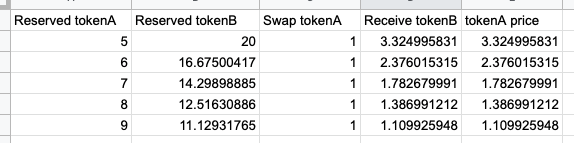
Why would tokenA’s price drop when Tim swaps tokenA for tokenB? I think this is to follow the law of supply and demand: selling a token would make its price drop, and buying a token would make its price rise.
So if Tim was to swap 4 tokenB for tokenA, then he would receive 0.81239531 tokenA, which is calculated as 5 – 5 * 20 / ((20 + 4) — 4 * 0.03) (with V1’s formula). The swap changed tokenA’s price from 4 tokenB to about 4.9237 tokenB (4/0.8124).
Note, Uniswap also provides public read methods to calculate the exact token amount to be received from swapping:
Market price and Arbitrageurs
In the beginning of the example, we assumed the market price of tokenA is the same as the liquidity pool before Tim swaps tokens. In fact, for a popular liquidity pool, the token price usually is very close to the market price.
Why? Because if the token price is off the market, there will be arbitrageurs acquiring tokens from other market with low cost, and swap with the liquidity pool to make a profit.
Arbitrageurs are mostly bots. Since decentralized exchanges allow anyone to swap tokens, there are lots of Arbitrageur bots monitoring liquidity pools to find arbitrage opportunities. Therefore, when a trader queries the token price of a liquidity pool, especially for a popular token pair, the price mostly likely matches the market price.
Front running
The Uniswap transactions can be front run to certain extend. Since miners, who build blocks, can decide the order of transactions in the block they are building. They could add swap transactions before yours (front running) to make a profit.
In order to minimize the front running issue, Uniswap introduced amountOutMin and deadline arguments to the swap methods, so that if there are front running transactions or race condition that caused the output amount token to be less than the specified amountOutMin, then the transaction would revert, and no token is transferred. In addition to that, if the transaction is included in a block after the specified deadline block, then the transaction would also revert.
Wrapped Ethereum
swapExactTokensForTokens allows traders to swap between ERC-20 tokens. However, it can’t be used to swap between ETH and ERC-20 tokens, because the native ETH token is not a ERC-20 token, as it was built before the ERC-20 standard existed. In order to support ETH-ERC-20 swapping, Uniswap provided swapExactTokensForETH and swapTokensForExactETH methods. They will convert ETH into WETH (wrapped ETH), which is a ERC-20 token, so that the WETH tokens can be used for swapping. And traders can withdraw the original ETH by sending WETH back to the WETH contract.
In summary,
swapExactETHForTokens will deposit ETH to WETH contract and receive WETH tokens, which will then be swapped to other tokens.
swapExactTokensForETH does the opposite: it swaps input tokens to WETH first, and then withdraw ETH from the WETH contract with the WETH tokens.
Liquid Providers
OK, we’ve learned what Uniswap V2 provides to allow traders to swap ERC-20 tokens. But this is just one side of the market. Uniswap still needs a way to incentivize someone to deposit their tokens into the liquidity pool so that traders can swap, otherwise the liquidity pool would have no tokens, and no trader would use the contract.
Uniswap calls them Liquid Providers who are incentivized to deposit tokens into the pool and create the market for traders to swap tokens.
Uniswap incentivizes liquid providers with a fixed 0.3% fee to be earned for each swap transaction.
But here are the questions:
- When does the fee get transferred to the liquid providers?
- If there are multiple liquid providers, how is the fee divided between them?
- How does liquid provider redeem their tokens including the earned fees?
Instead of answering these question individually, I will walk you through an example with concrete numbers to explain. If you have the same questions as above, keep them in mind when reading through!
Example — Liquidity Provider adding Liquidity
Lisa adds liquidity
Let’s start from scratch. Initially the tokenA-tokenB pool doesn’t exist. Liquid provider Lisa adds 5 tokenA and 20 tokenB to create this pool. Now the pool has 5 tokenA and 20 tokenB. In return, the pool will mint 10 pool share tokens and transfer them to Lisa as a proof of ownership. Let’s call this pool share tokens “tokenP”.
TokenP are minted to track the relative proportion of total reserved that each liquidity provider has contributed. Since Lisa is the first and the only liquidity provider of the pool, she owns 100% of the tokens in the pool.
To make it easy to see how tokens are moved between accounts after each transaction, I made the following table that shows the token ownership changes:
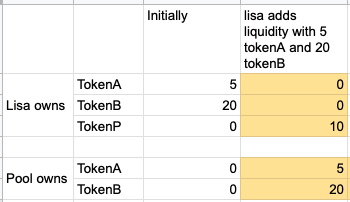
Note, tokenP is also a ERC-20 token, which can also be transferred or swapped, just like any other ERC-20 tokens.
But why adding 5 tokenA and 20 tokenB would mint 10 tokenP? How is the amount 10 calculated?
It is calculated as the square root of the input amount of tokenA times the input amount of tokenB, which is the square root of 5 * 20, resulting in10.
Why did Lisa add tokens with 1:4 ratio? Why not adding 5 tokenA and 10 tokenB instead, which is 1:2 ratio, or some other ratio?
That’s because Lisa knows 1:4 is the market ratio: 1 tokenA is worth 4 tokenB. If she adds 5 tokenA and 10 tokenB instead, then there will be arbitrageurs swapping tokens thus making a profit until the pool has remaining tokens with a 1:4 ratio. So the first Liquid Provider will add tokens.
Lily adds liquidity
Now let’s see what happens when there are multiple liquidity providers adding tokens to the liquidity pool.
If Lily adds 50 tokenA and 200 tokenB to the pool after Lisa, then Lily will receive 100 tokenP, which is the square root of 50 * 200. Since there are additional 100 tokenP minted, the total supply of tokenP has increased to 110, among which Lisa owns about 9.09091% (1/11), and Lily owns the rest 90.90909%(10/11). These percentages will determine how many tokens they can redeem from the pool when they remove liquidity.
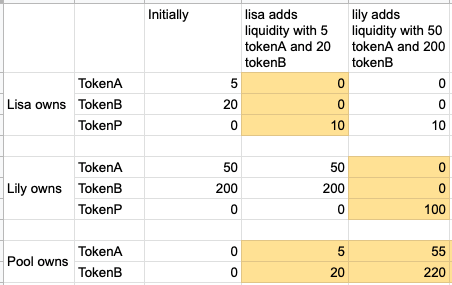
You might wonder, what if Lily tries to be foxy here: what if she adds 25 tokenA and 400 tokenB? Wouldn’t that mint the same amount of tokenP since the square root of 50*200 and 25*400 are the same?
Uniswap has considered this case and will prevent it by punishment.
If tokens are added to the pool with a different ratio, then the minted tokens can not accurately represent the liquidity provider’s share. In order to address this issue, Uniswap introduced a rule such that, if the token ratio is different from the existing ratio in the pool, the liquid provider will end up receiving less liquidity tokens as a punishment.
For instance, since the current token ratio in the pool is 1:4, by adding 25 tokenA and 400 tokenB, Lily will receive the same amount of tokenP as sending 25 tokenA and 100 tokenB, which is only 50 tokenP. Likewise, by adding 100 tokenA and 100 tokenB, she will receive the same amount of tokenP as sending 25 tokenA and 100 tokenB, which is also only 50 tokenP. If the ratio is not the same as what the pool currently has, then there are always some tokens wasted in the sense that those tokens were added to the pool but no additional liquidity tokens were minted to the liquidity provider.
With this rule, the liquidity providers are incentivized to add tokens at the same ratio as the pool. And we know the rate is always close to the market price otherwise Arbitrageurs will arbitrage if the token ratio was off the market.
Great! Now both Lisa and Lily have added their pairs of tokens to the liquidity pool and received the liquidity tokens as shares of ownership. Let’s continue to see what happens when tokens in the pool are swapped by Traders.
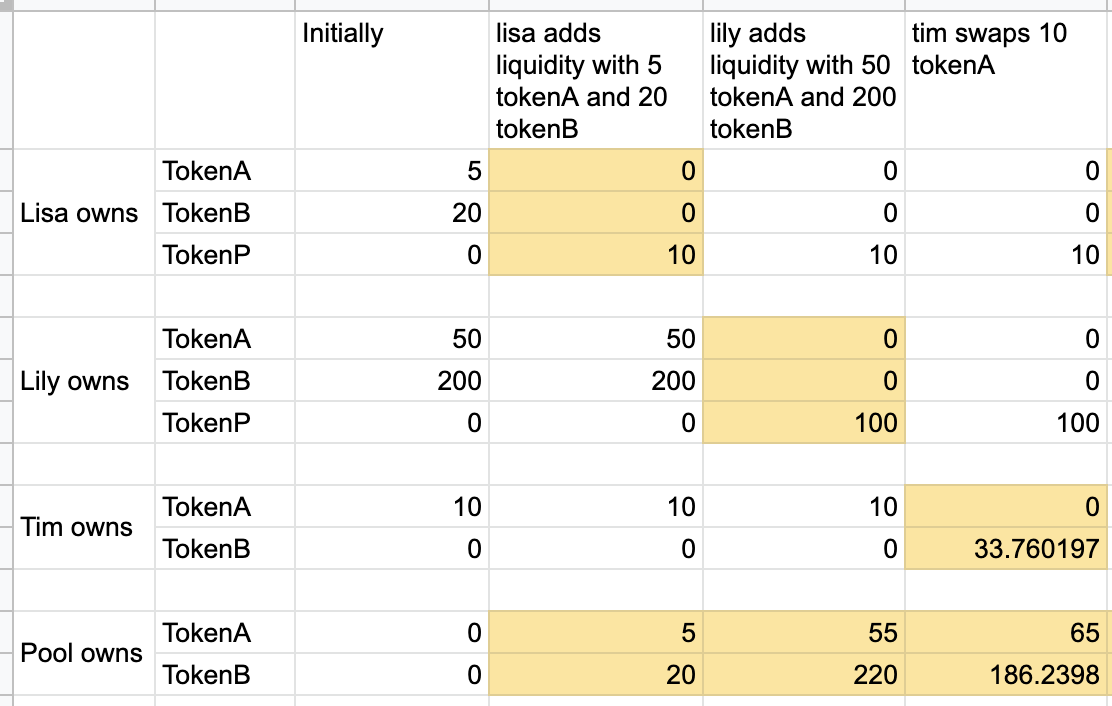
Tim swaps tokens
With 55 tokenA and 220 tokenB in the pool, now Trader Tim swaps 10 tokenA which will transfer to him 33.333 tokenB. After the swap, the pool has 65 tokenA and 186.2398 tokenB. We did not repeat the calculation steps here for this swap, since we’ve explained it earlier.
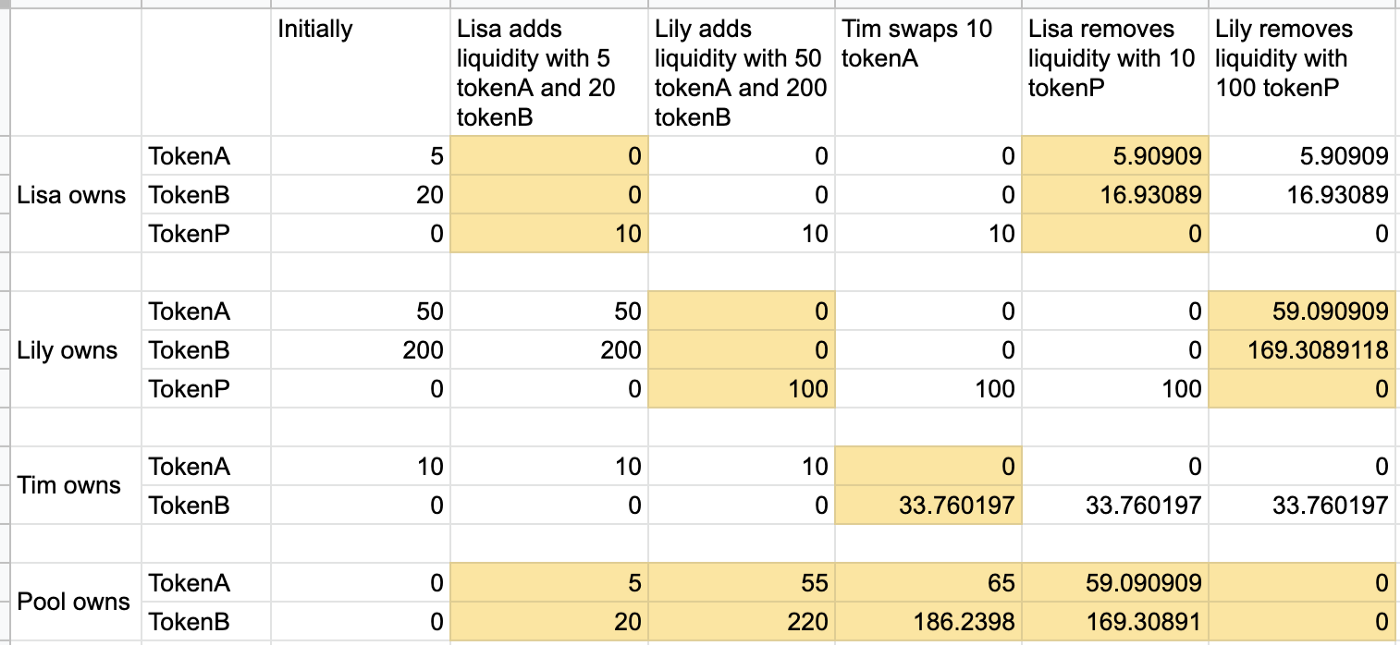
Lisa removes liquidity
Now Lisa decides to redeem all of her tokens. In order to do that, she needs to call the removeLiquidity method. The removeLiquidity method burns the liquidity tokens in exchange for the underlying tokens. Since Lisa decides to redeem max amount, she transfers to the pool all her 10 tokenP, which will be burned, and Lisa will receive 5.90909 tokenA (65 * 9.090909%) and 16.93089 (186.2398 * 9.090909%) tokenB. After Lisa redeemed her tokens from the pool, now the token has 59.090909 tokenA and 169.30891 tokenB left.

Lily removes Liquidity
After Lisa remove all of her tokens, Lily also decides to redeem. She called removeLiquidity with all her 100 tokenP. The pool burns them and transfer 59.090909 tokenA and 169.30891 tokenB to Lily. Now, the pool has no tokenA and tokenB left (technically there is a tiny amount of each token locked to prevent issues like dividing by 0, but the amount is so small that it could be ignored. If you are interested in those details, you can see them by running my test case posted in the end).
All right, we’ve walked through the example of adding liquidity to the pool, swapping tokens and removing liquidity from the pool.
Summary
This post explained how the math works in Uniswap V2 contract when tokens are added, swapped and removed from the liquidity pool. There are some details in the calculation that I chose to simplify in order to keep it beginner-friendly. If you are interested in those details, including the actual on-chain calculation that uses uint32 numbers, you can check out contract source code, as well as my test cases which implemented the above examples.
Uniswap V2 also provides other features like Flash Swaps, and improves price oracle, etc, which are not covered in this post. If you are interested, you can read the whitepaper.


